Plotting on the Bloch Sphere
Introduction
When studying the dynamics of a two-level system, it is often convenient to visualize the state of the system by plotting the state-vector or density matrix on the Bloch sphere. In QuTiP, there is a class to allow for easy creation and manipulation of data sets, both vectors and data points, on the Bloch sphere.
The Bloch Class
In QuTiP, creating a Bloch sphere is accomplished by calling either:
b = qutip.Bloch()
which will load an instance of the Bloch class.
Before getting into the details of these objects, we can simply plot the blank Bloch sphere associated with these instances via:
b.make_sphere()
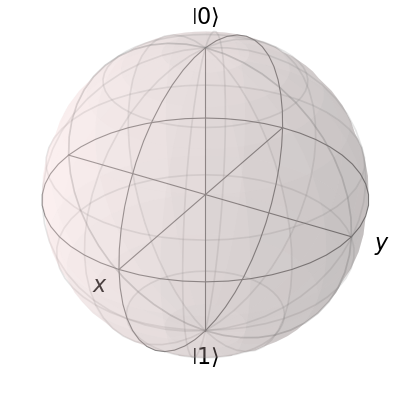
In addition to the show command, see the API documentation for Bloch for a full list of other available functions.
As an example, we can add a single data point:
pnt = [1/np.sqrt(3), 1/np.sqrt(3), 1/np.sqrt(3)]
b.add_points(pnt)
b.render()
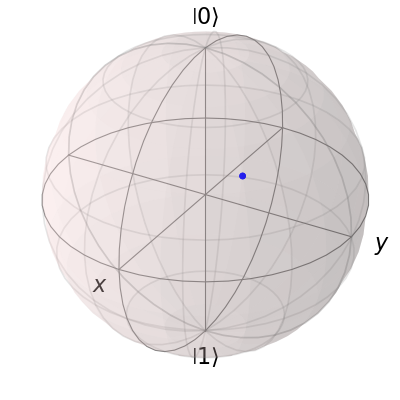
and then a single vector:
b.fig.clf()
vec = [0, 1, 0]
b.add_vectors(vec)
b.render()
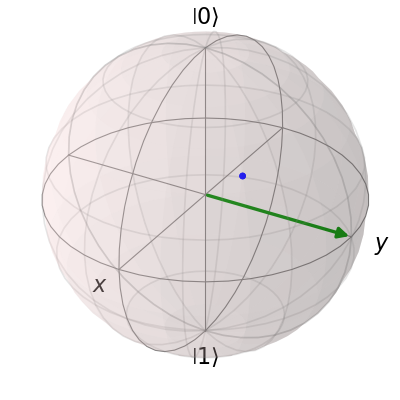
and then add another vector corresponding to the \(\left|\rm up \right>\) state:
up = qutip.basis(2, 0)
b.add_states(up)
b.render()
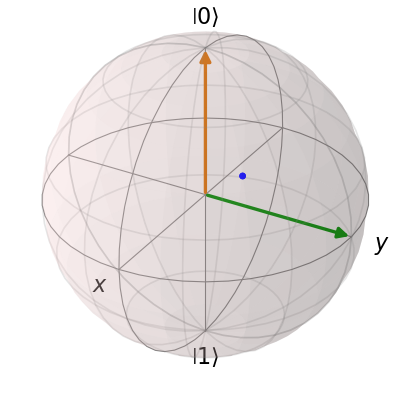
Notice that when we add more than a single vector (or data point), a different color will automatically be applied to the later data set (mod 4). In total, the code for constructing our Bloch sphere with one vector, one state, and a single data point is:
b = qutip.Bloch()
pnt = [1./np.sqrt(3), 1./np.sqrt(3), 1./np.sqrt(3)]
b.add_points(pnt)
vec = [0, 1, 0]
b.add_vectors(vec)
up = qutip.basis(2, 0)
b.add_states(up)
b.render()
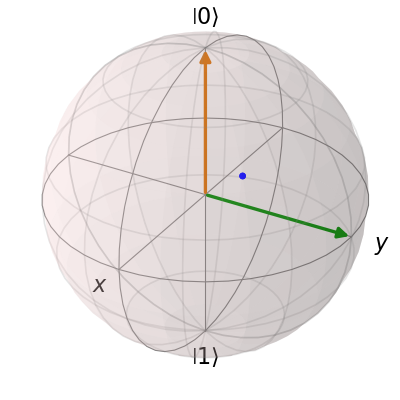
where we have removed the extra show() commands.
We can also plot multiple points, vectors, and states at the same time by passing list or arrays instead of individual elements. Before giving an example, we can use the clear() command to remove the current data from our Bloch sphere instead of creating a new instance:
b.clear()
b.render()
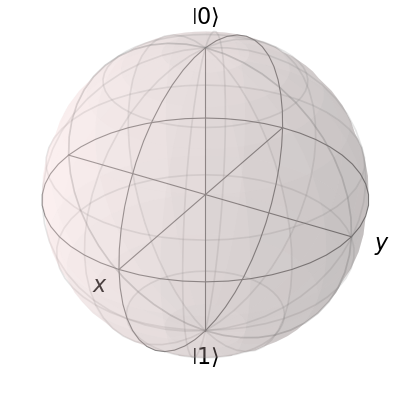
Now on the same Bloch sphere, we can plot the three states associated with the x, y, and z directions:
x = (qutip.basis(2, 0) + (1+0j)*qutip.basis(2, 1)).unit()
y = (qutip.basis(2, 0) + (0+1j)*qutip.basis(2, 1)).unit()
z = (qutip.basis(2, 0) + (0+0j)*qutip.basis(2, 1)).unit()
b.add_states([x, y, z])
b.render()
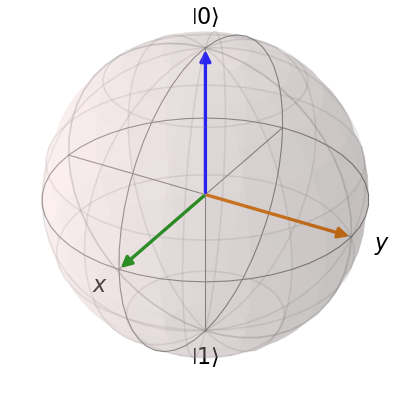
a similar method works for adding vectors:
b.clear()
vec = [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
b.add_vectors(vec)
b.render()
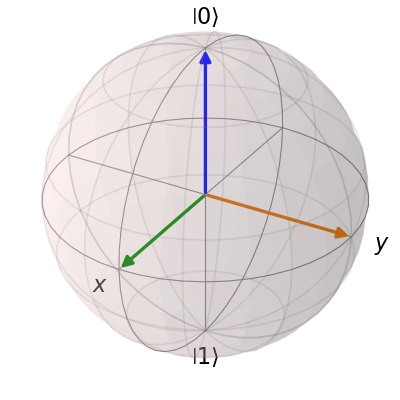
Adding multiple points to the Bloch sphere works slightly differently than adding multiple states or vectors. For example, lets add a set of 20 points around the equator (after calling clear()):
b.clear()
th = np.linspace(0, 2*np.pi, 20)
xp = np.cos(th)
yp = np.sin(th)
zp = np.zeros(20)
pnts = [xp, yp, zp]
b.add_points(pnts)
b.render()
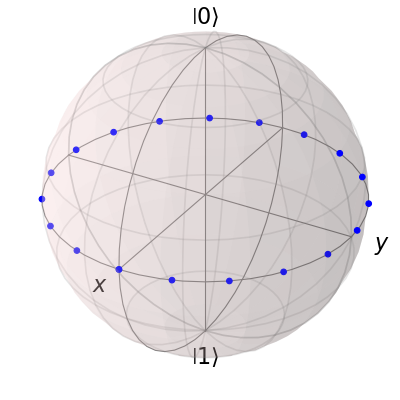
Notice that, in contrast to states or vectors, each point remains the same color as the initial point. This is because adding multiple data points using the add_points function is interpreted, by default, to correspond to a single data point (single qubit state) plotted at different times. This is very useful when visualizing the dynamics of a qubit. An example of this is given in the example . If we want to plot additional qubit states we can call additional add_points functions:
xz = np.zeros(20)
yz = np.sin(th)
zz = np.cos(th)
b.add_points([xz, yz, zz])
b.render()
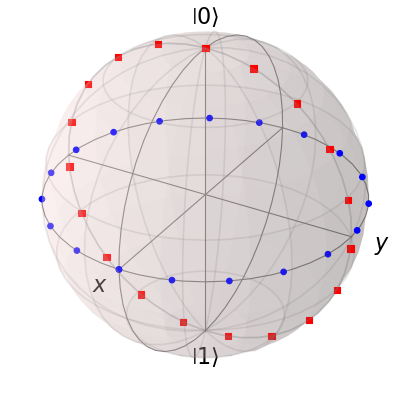
The color and shape of the data points is varied automatically by the Bloch class. Notice how the color and point markers change for each set of data. Again, we have had to call add_points twice because adding more than one set of multiple data points is not supported by the add_points function.
What if we want to vary the color of our points. We can tell the qutip.bloch.Bloch class to vary the color of each point according to the colors listed in the b.point_color list (see Configuring the Bloch sphere below). Again after clear():
b.clear()
xp = np.cos(th)
yp = np.sin(th)
zp = np.zeros(20)
pnts = [xp, yp, zp]
b.add_points(pnts, 'm') # <-- add a 'm' string to signify 'multi' colored points
b.render()
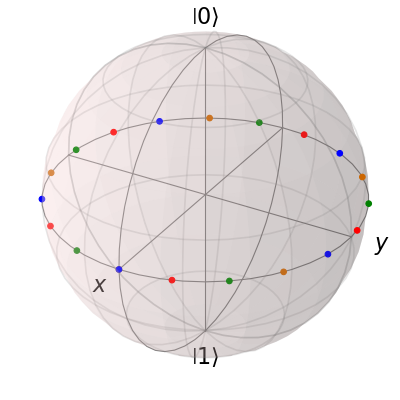
Now, the data points cycle through a variety of predefined colors. Now lets add another set of points, but this time we want the set to be a single color, representing say a qubit going from the \(\left|\rm up\right>\) state to the \(\left|\rm down\right>\) state in the y-z plane:
xz = np.zeros(20)
yz = np.sin(th)
zz = np.cos(th)
b.add_points([xz, yz, zz]) # no 'm'
b.render()
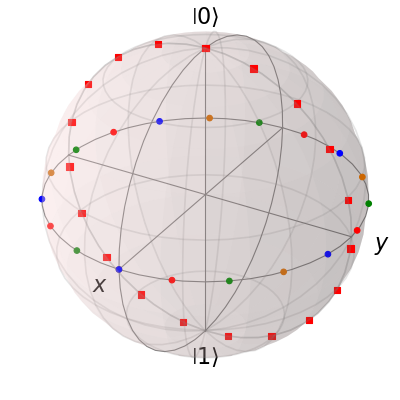
A more slick way of using this ‘multi’ color feature is also given in the example, where we set the color of the markers as a function of time.
Configuring the Bloch sphere
Bloch Class Options
At the end of the last section we saw that the colors and marker shapes of the data plotted on the Bloch sphere are automatically varied according to the number of points and vectors added. But what if you want a different choice of color, or you want your sphere to be purple with different axes labels? Well then you are in luck as the Bloch class has 22 attributes which one can control. Assuming b=Bloch():
Attribute |
Function |
Default Setting |
|---|---|---|
b.axes |
Matplotlib axes instance for animations. Set by |
|
b.fig |
User supplied Matplotlib Figure instance. Set by |
|
b.font_color |
Color of fonts |
‘black’ |
b.font_size |
Size of fonts |
20 |
b.frame_alpha |
Transparency of wireframe |
0.1 |
b.frame_color |
Color of wireframe |
‘gray’ |
b.frame_width |
Width of wireframe |
1 |
b.point_color |
List of colors for Bloch point markers to cycle through |
|
b.point_marker |
List of point marker shapes to cycle through |
|
b.point_size |
List of point marker sizes (not all markers look the same size when plotted) |
|
b.sphere_alpha |
Transparency of Bloch sphere |
0.2 |
b.sphere_color |
Color of Bloch sphere |
|
b.size |
Sets size of figure window |
|
b.vector_color |
List of colors for Bloch vectors to cycle through |
|
b.vector_width |
Width of Bloch vectors |
4 |
b.view |
Azimuthal and Elevation viewing angles |
|
b.xlabel |
Labels for x-axis |
|
b.xlpos |
Position of x-axis labels |
|
b.ylabel |
Labels for y-axis |
|
b.ylpos |
Position of y-axis labels |
|
b.zlabel |
Labels for z-axis |
|
b.zlpos |
Position of z-axis labels |
|
These properties can also be accessed via the print command:
>>> b = qutip.Bloch()
>>> print(b)
Bloch data:
-----------
Number of points: 0
Number of vectors: 0
Bloch sphere properties:
------------------------
font_color: black
font_size: 20
frame_alpha: 0.2
frame_color: gray
frame_width: 1
point_color: ['b', 'r', 'g', '#CC6600']
point_marker: ['o', 's', 'd', '^']
point_size: [25, 32, 35, 45]
sphere_alpha: 0.2
sphere_color: #FFDDDD
figsize: [5, 5]
vector_color: ['g', '#CC6600', 'b', 'r']
vector_width: 3
vector_style: -|>
vector_mutation: 20
view: [-60, 30]
xlabel: ['$x$', '']
xlpos: [1.2, -1.2]
ylabel: ['$y$', '']
ylpos: [1.2, -1.2]
zlabel: ['$\\left|0\\right>$', '$\\left|1\\right>$']
zlpos: [1.2, -1.2]
Animating with the Bloch sphere
The Bloch class was designed from the outset to generate animations. To animate a set of vectors or data points the basic idea is: plot the data at time t1, save the sphere, clear the sphere, plot data at t2,… The Bloch sphere will automatically number the output file based on how many times the object has been saved (this is stored in b.savenum). The easiest way to animate data on the Bloch sphere is to use the save() method and generate a series of images to convert into an animation. However, as of Matplotlib version 1.1, creating animations is built-in. We will demonstrate both methods by looking at the decay of a qubit on the bloch sphere.
Example: Qubit Decay
The code for calculating the expectation values for the Pauli spin operators of a qubit decay is given below. This code is common to both animation examples.
import numpy as np
import qutip
def qubit_integrate(w, theta, gamma1, gamma2, psi0, tlist):
# operators and the hamiltonian
sx = qutip.sigmax()
sy = qutip.sigmay()
sz = qutip.sigmaz()
sm = qutip.sigmam()
H = w * (np.cos(theta) * sz + np.sin(theta) * sx)
# collapse operators
c_op_list = []
n_th = 0.5 # temperature
rate = gamma1 * (n_th + 1)
if rate > 0.0: c_op_list.append(np.sqrt(rate) * sm)
rate = gamma1 * n_th
if rate > 0.0: c_op_list.append(np.sqrt(rate) * sm.dag())
rate = gamma2
if rate > 0.0: c_op_list.append(np.sqrt(rate) * sz)
# evolve and calculate expectation values
output = qutip.mesolve(H, psi0, tlist, c_op_list, [sx, sy, sz])
return output.expect[0], output.expect[1], output.expect[2]
## calculate the dynamics
w = 1.0 * 2 * np.pi # qubit angular frequency
theta = 0.2 * np.pi # qubit angle from sigma_z axis (toward sigma_x axis)
gamma1 = 0.5 # qubit relaxation rate
gamma2 = 0.2 # qubit dephasing rate
# initial state
a = 1.0
psi0 = (a*qutip.basis(2, 0) + (1-a)*qutip.basis(2, 1))/np.sqrt(a**2 + (1-a)**2)
tlist = np.linspace(0, 4, 250)
#expectation values for ploting
sx, sy, sz = qubit_integrate(w, theta, gamma1, gamma2, psi0, tlist)
Generating Images for Animation
An example of generating images for generating an animation outside of Python is given below:
import numpy as np
b = qutip.Bloch()
b.vector_color = ['r']
b.view = [-40, 30]
for i in range(len(sx)):
b.clear()
b.add_vectors([np.sin(theta), 0, np.cos(theta)])
b.add_points([sx[:i+1], sy[:i+1], sz[:i+1]])
b.save(dirc='temp') # saving images to temp directory in current working directory
Generating an animation using FFmpeg (for example) is fairly simple:
ffmpeg -i temp/bloch_%01d.png bloch.mp4
Directly Generating an Animation
Important
Generating animations directly from Matplotlib requires installing either MEncoder or FFmpeg.
While either choice works on linux, it is best to choose FFmpeg when running on the Mac.
If using macports just do: sudo port install ffmpeg.
The code to directly generate an mp4 movie of the Qubit decay is as follows
from matplotlib import pyplot, animation
from mpl_toolkits.mplot3d import Axes3D
fig = pyplot.figure()
ax = Axes3D(fig, azim=-40, elev=30)
sphere = qutip.Bloch(axes=ax)
def animate(i):
sphere.clear()
sphere.add_vectors([np.sin(theta), 0, np.cos(theta)])
sphere.add_points([sx[:i+1], sy[:i+1], sz[:i+1]])
sphere.make_sphere()
return ax
def init():
sphere.vector_color = ['r']
return ax
ani = animation.FuncAnimation(fig, animate, np.arange(len(sx)),
init_func=init, blit=False, repeat=False)
ani.save('bloch_sphere.mp4', fps=20)
The resulting movie may be viewed here: bloch_decay.mp4